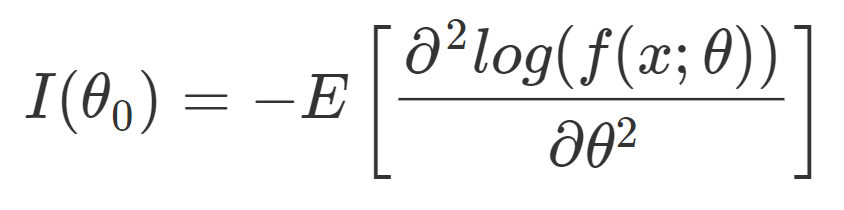Method of Moments and Maximum Likelihood Estimation
One of the fundamental goals of statistics is to draw inferences about a population using observed data. The parameters of a population are almost always unknown, so to draw valid inferences, they need to be estimated with as much accuracy as possible. Method of moments estimation and maximum likelihood estimation are two powerful mechanisms that can accomplish this task.
What is the Method of Moments Estimator (MoM)?
A distribution’s moments contain information about several of its characteristics, including its center, shape, and skew. The first moment (expected value or population mean) is frequently a function of the distribution’s parameters, and when the data is assumed to be independent and identically distributed, the sample mean is an unbiased estimate of the first moment. This technique of parameter estimation can usually be calculated pretty quickly, but it can be shown that maximum likelihood estimation performs better.
What is Maximum Likelihood Estimation (MLE)?
The likelihood function of a distribution describes the probability of observing a specific outcome in terms of the distribution’s parameters, and when the data is independent and identically distributed, the likelihood function is easy to work with. The maximum likelihood estimator is found by maximizing the log of the likelihood function with respect to the parameter of interest. In some distributions, we get a closed-form solution for the maximum likelihood, but numerical methods are frequently required to obtain the estimated parameter.
Since both the method of moments estimator and maximum likelihood estimator are calculated using random variables (observed data), they also are random variables and therefore have a distribution. In accordance with the central limit theorem, the parameter estimates have a normal distribution with a sufficiently large sample size. The distributions of the method of moments and maximum likelihood estimators both have a mean of the true parameter, but they may have different variances.
Continuous Mapping Theorem
The asymptotic variance of the method of moments estimator can be calculated by using the continuous mapping theorem. Since the parameter of interest is often a function of the sample mean, we can reparameterize the equation to calculate the variance of the method of moments estimator.
Fisher Information and the Cramér-Rao Bound
Formula for the Fisher information of a distribution.
The asymptotic variance for the maximum likelihood estimator uses the inverse of the distribution’s Fisher information. The Fisher information quantifies how much information a random variable carries about a distribution’s parameter(s). The Cramér-Rao bound states that the asymptotic variance of an unbiased estimator must be greater than or equal to the inverse of the Fisher information.
*The continuous mapping theorem and Fisher information may seem ambiguous without seeing an example. The step-by-step derivations of both estimators and variances for the binomial distribution and gamma distribution can be found on my Github.
Which estimator is better?
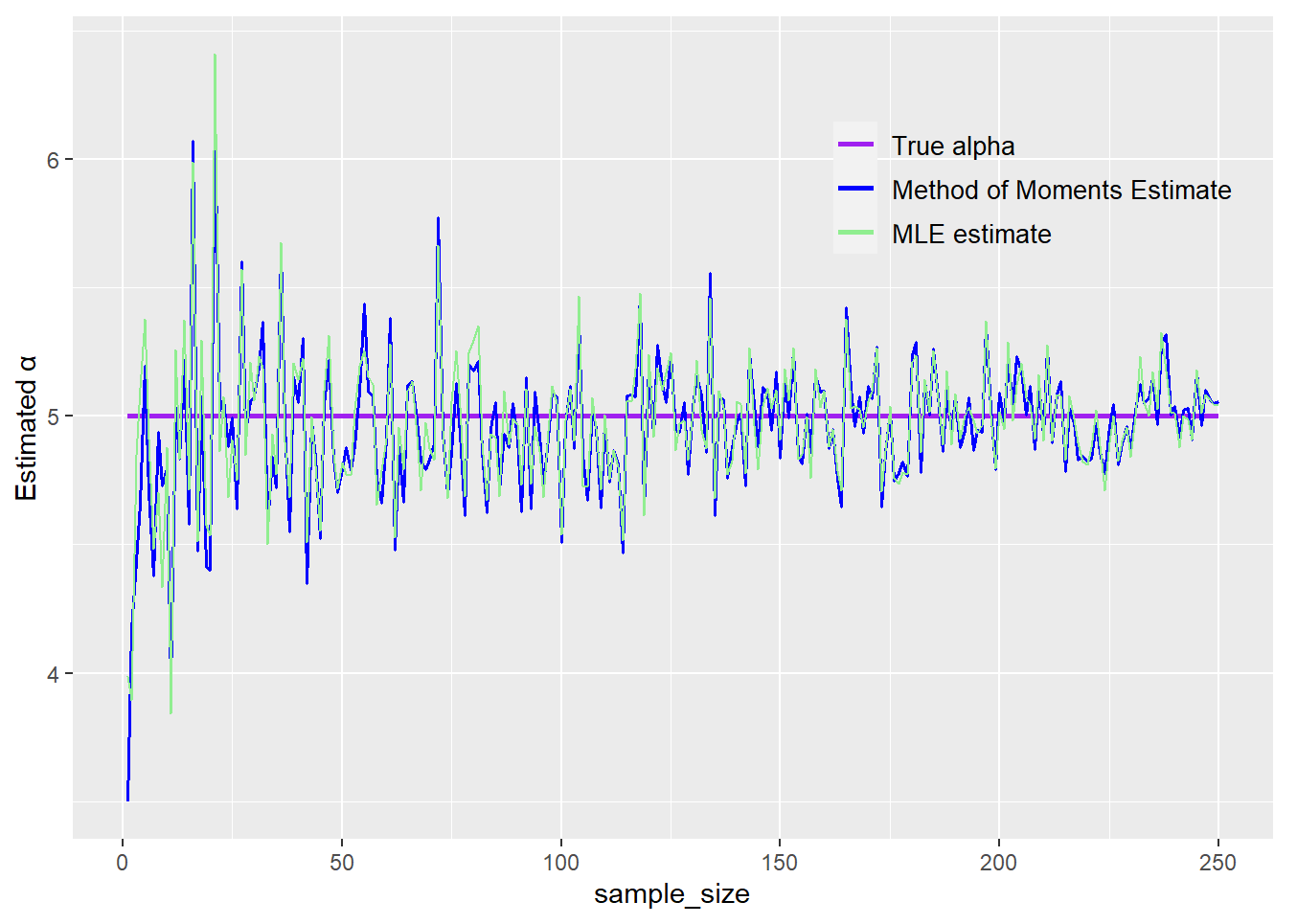
Although the method of moments estimator is usually quicker to calculate, it is never more precise than the maximum likelihood estimator with a sufficiently large sample size. However, as demonstrated in the gamma distribution example of my simulation, the method of moments estimator can have a closed-form solution and can be calculated much more quickly at the expense of a slightly higher variance than the maximum likelihood estimator.
Observe how the estimates approach the true value of the parameter as the sample size gets larger. Also, observe how the method of moments estimator appears to vary slightly more than the maximum likelihood estimator.
Method of moments and maximum likelihood estimation both rely on the assumption that the underlying distribution is known, and in many datasets, this assumption may be difficult to make. These methods may not always be applicable, but are still very powerful statistical tools that can be extremely accurate under the right circumstances.