How Neural Networks Learn
Neural Networks are some of the most interesting and exciting algorithms in machine learning, but they can also be the most daunting to comprehend. Two courses in my undergraduate Statistics program discussed neural networks, and they took divergent approaches: one focused on their implementation in the Keras-TensorFlow ecosystem in Python, whereas the other provided a rudimentary explanation of the math that enables their incredible predictive power. Despite learning a lot in these courses, I realized that until recently I found it quite challenging to explain the underlying concepts in a concise, simplistic manner. After consulting many resources and improving my own understanding, I now have an effective way to do so.
Emergent Garden has a great video that elaborates upon the importance of functions.
But before diving into the details, I think it's important to establish the motivations of a neural network. In its most primitive sense, the goal of a neural network is to approximate an unknown function. In order to conceptualize this, think of a simple function: a linear equation, f(x) = ax + b. A neural network would use x and f(x) to approximate a and b, essentially reverse engineering the function using inputs, x, and outputs, f(x). However, using a neural network to approximate these two values is ultimately pretty trivial, most people could estimate them just by looking at several points plotted in 2-dimensional space. Neural networks become more practical when the unknown function of interest is effectively impossible for humans, and even other machine learning models, to approximate.
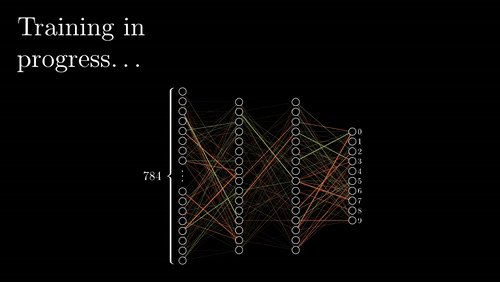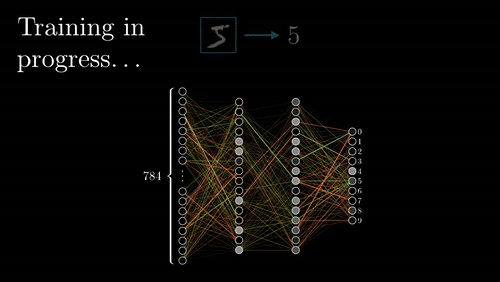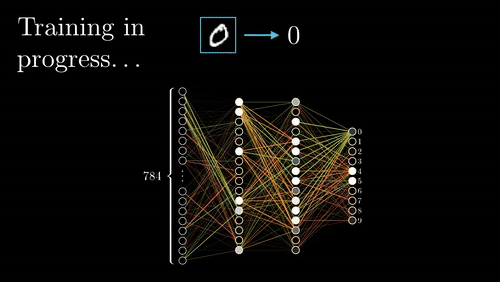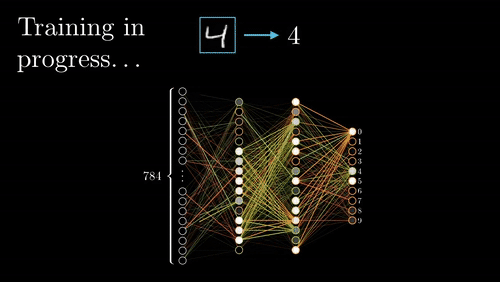
A basic neural network has one input layer, which contains the data we choose to give to the network, one output layer, which contains the predictions of the model, and one or more hidden layers, which serve as a liaison to find the unknown relationship between inputs and outputs. All layers contain a defined number of neurons, which use activation functions that are aggregated to approximate the main unknown function. These neurons use a linear combination of the previous layers’ output and parameters, weights and biases, that change as the network learns. You can imagine weights to be the strength of the connections between layers and bias as a neuron’s tendency to be active or inactive. Learning refers to the network tuning these weights and biases to minimize the number of times it gives inaccurate predictions.


Before explaining how the network learns, it’s important to explain how it arrives at a prediction in the first place. The neurons in the first hidden layer use an activation function that uses weights, the input layers outputs, and biases to express how “active” that neuron is (see Neural Network Linear Algebra image above). Each of these neurons then feeds forward their activation values to the next layer of neurons, which are then multiplied to a new set of weights and added to a bias term inside of the subsequent neurons’ own activation functions. This feeding forward process continues until the network reaches the output layer, where it then evaluates its success with a cost function.
We use a cost function to measure how close the network’s predicted value is to the actual value for each data point in our training dataset. If the predicted values are really close to the actual values, then our cost function returns a small value, and we have a good network; if our cost function returns a high value, we have an unreliable network. Training the network refers to the process of finding values of weights and biases that make the predicted values come closest on average to the true outcomes, therefore minimizing the cost function.
If you are familiar with calculus, you may recognize that this minimization problem can be approached by calculating the gradient of the cost function. The gradient basically means how sensitive the cost function is to each weight and bias throughout the entire network, and how each value should be adjusted to approach a local minimum. We adjust the weights and biases throughout the network according to the cost function’s gradient, then go back to the input layer and feed forward with our new and improved parameters. Ideally, the cost function will now yield a smaller value than the iteration before, meaning that our network is now more accurate. The network continuously iterates the process of forward (feeding) and backward propagation (calculating the cost function’s gradients), tuning the weights and biases, which adjusts the activation values of neurons. After this algorithm repeats enough times, the gradient will become smaller and smaller, and the weights and biases will effectively converge to a final value, giving the lowest cost the neural network can achieve with that specific initialization, structure, and training dataset.
Visualization of Forward and Back propagation via 3Blue1Brown
Although I covered the essentials of neural networks, there are some details that I omitted for the sake of brevity and simplicity; many researchers have written entire books detailing the mathematical theory, applications, and variations of neural networks. The explanation I gave covered a simple neural network, and although many networks today are much more complex, they still use similar concepts. If you find this topic interesting, I suggest looking through the following resources:
3Blue1Brown has been a great resource while writing this post. They have a 4-episode mini-series on YouTube that gives great descriptions and diagrams about the fundamentals of Neural Networks. The entire series is about an hour and is definitely worth the watch!
Create and train your own neural network:
Annotated Python code implementing neural network with only NumPy
More detailed explanations of concepts I mentioned: